Powrócę do słynnego doświadczenia Michelsona – Morleya wykonanego w 1881 roku, który zasłynął tym, że nie można było zrozumieć dlaczego otrzymany obraz światła w detektorze nie jest przesunięty w fazie. Wnioski z tłumaczenia tego doświadczenia i mnie nie dawały spokoju przez lata. W książce Rzeczywistość w świetle nauki, filozofii i wiary JEDNOŚĆ 2008 roku opisałem to doświadczenie bazując na tłumaczeniu A. Einsteina, który skorzystał ze skrócenia długości FitzGeralda i transformacji Lorentza. Jak pisałem:

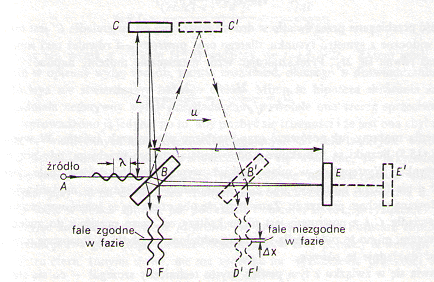
Doświadczenie polegało na tym, że puszczano promienie światła w dwóch kierunkach – wzdłuż kierunku ruchu przyrządu i prostopadle do ruchu. Według fizyki klasycznej wyprowadzono dwa wzory na czas powrotu promieni odbitych. Były one różne, bo po podstawieniu wartości dawały różne wyniki. Spodziewano się więc, że w czasie doświadczenia przyrząd potwierdzi wyliczone różnice czasowe tych dwóch promieni. A tu niespodzianka. Czasy były takie same. Wynik doświadczenia M-M był bardzo zagadkowy i w najwyższym stopniu zaskakujący.

          Czasy obu promieni były różne, bo drogi przyjęto różne. W tym tkwiła pomyłka. Ona spowodowała, że wysunięto zbyt pochopne wnioski.

          Na rysunku linią przerywaną pokazana jest droga promienia prostopadłego do ruchu aparatury. Na rysunku nakreślono drogę promienia po trójkącie. Wszelakie obliczenia i wnioski bazowały na przyjętej tezie. Tymczasem promień prostopadły do ruchu utrzymuje cały czas drogę prostopadłą do ruchu urządzenia. Promień odbija się od lustra już przesuniętego, i wraca pionowo do samego detektora również przesuniętego. Kwant promienia przebywa drogę 2L, a nie jak w oficjalnym tłumaczeniu po ramionach trójkąta (dłuższa droga).  Promień biegnący równolegle przebywa tę samą drogę 2L (tam i z powrotem) w tym samym czasie, ze średnią prędkością (pozorną) równą c, bo prędkość urządzenia się znosi (+u, -u) w drodze powrotnej.  Równe czasy przebiegu, z tą samą prędkością, na podobnej drodze nie może powodować niezgodności w fazie. Zagadka jest rozwiązana. Tłumaczenie powyższe bardzo dobrze można udowodnić animacją filmową, na którym pokazano by drogą zaznaczonego kwantu.  Pomijam tu sprawę, wówczas bardzo ważną, tzw. eteru, ale w podanym tłumaczeniu nie odgrywa on żadnej roli.

         Zachodzi pytanie, dlaczego Einstein nie poszedł podobną ścieżką rozumowania? Jest ona klarowna i prosta.  Można pomyśleć, że Einstein się pomylił. Ryzykowna teza, ale wszystko wskazuje, że jest słuszna.

          W książce Filozofia w Fizyce Jarosława Kukowskiego  WU Kardynała Wyszyńskiego Warszawa 2000 r. (s. 71) autor powołuje się na publikację Turzynieckiego z 1993 roku. W niej znalazłem podobny wniosek, choć Turzyniecki poprowadził obliczenia, tak samo po trójkącie, rezygnując z postulatu Einsteina, że prędkość światła jest stała i niezmienna . Wiele lat temu odrzuciłem rozumowanie Turzynieckiego, bo postulat Einsteina uważałem i nadal uważam za słuszny. Ja go tylko inaczej opisuję, a mianowicie, światło gdy opuszcza swoje źródło ma zawsze tę samą prędkość < c > względem każdego układu inercjalnego i jest niezależny od prędkości źródła. Światło nie zachowuje prędkości źródła. Dla układów w ruchu przyjmuje prędkość pozorną. Ona może być różna od prędkości < c > Dopuszczalne jest więc założenie, że c’ = c + u. Taki wzór przyjął w swej książce Turzyniecki.

          Podejście Turzynieckiego i tu zaprezentowane skutkuje, że nie trzeba angażować do wyjaśnienia negatywnego doświadczenia transformacji Lorentza, a co za tym idzie, wnioski wysuwane o kontrakcji długości FitzGeralda  i dylatacji czasu są mylące. Jak pisze autor książki (J. Kukowski): “idea skrócenia autorstwa FitzGeralda0 LOrentza była hipotezą ratunkową w obliczu nieoczekiwanych wyników doświadczenia Michelsona- Morleya” (s 73).

          Wniosek ten nie obala teorii względności Einsteina, ale usuwa z niej niezrozumiałe zjawisko skracania długości. Problem pozostaje z dylatacją czasu, bo inne doświadczenia potwierdzają to zjawisko i póki co, wydaje się, że teza jest słuszna.