Wzór Einsteina E=m*c² znają wszyscy. Przedstawię wyprowadzenie tej formuły opisanej w książce: “Elementy Teorii Względności” Mieczysław Sawicki WSiP Warszawa 1975 r.
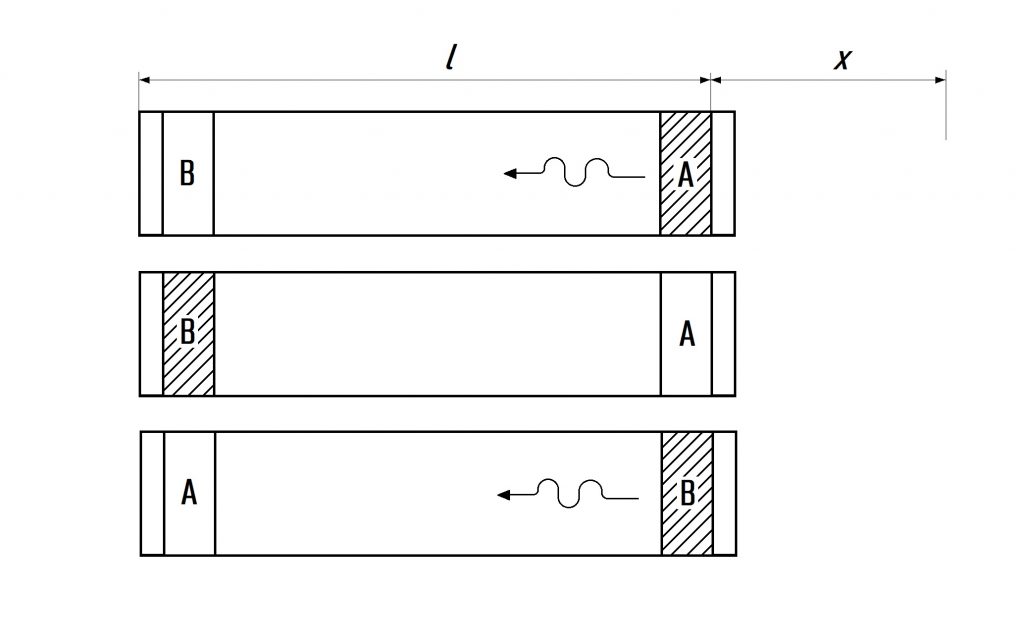
W tym celu skorzystamy z rysunku na którym znajdują się dwa identyczne ciała A i B. Załóżmy, że ciało A posiada pewien nadmiar energii w stosunku o ciał B. Energię tę ciało A emituje w postaci promieniowania wyłącznie w kierunku ciała B. Wskutek tego następuje “odrzut” i ciało A uzyskuje pęd w wielkości:
p = E/c
Jeżeli jest ono związane z rurą o masie M, to rura uzyskuje prędkość v według wzoru:
Mv = E/c wzór na pęd ciała M o prędkości v
stąd
v = E/Mc
i zwróconą w stronę przeciwną. Ruch rury trwa do momentu pochłonięcia energii przez ciało B. A więc w czasie
t = l/c
rura doznała przemieszczenia
x = vt
Po podstawieniu za t i v uzyskuje się
x = El/ Mc² (1)
Następnie przedstawiany ciało A na miejsce B i odwrotnie. Żadne siły zewnętrzne przy tym nie działają na układ A, B, M, wobec tego układ jako całość nie doznał przemieszczenia. Powtarzając ten proces moglibyśmy więc, bez udziału sił zewnętrznych, zmienić położenie środka masy układu ciał A,B M. Stałoby to w sprzeczności z podstawowymi prawami mechaniki. Wyjście z tej sytuacji jest jedno: przypuścić mianowicie, że obydwa ciała A i B po akcie emisji i absorpcji energii promieniowania nie są mechanicznie równoważne. Na przykład masa ciała B jest większa o wartość m od masy ciała A. W tym przypadku przy zamianie miejscami ciał masa m przesunie się o odcinek l. Stosując zasadę zachowania pędu twierdzimy, że pęd całkowity składający się z pędu rury
Mx/t
oraz pędu masy m
ml/t
jest równy zero
Mx/t – ml/t = 0
stąd x= ml/M (2)
Porównując związki (1) i (2) dostajemy
ml/M = lE/Mc²
skąd
m = E/c²
czyli E = m*c²
W tłumaczeniu własnym uproszczonym:
Pęd rury M (odrzut) = pęd nadmiaru masy (pęd emitowanej fali)
M * v = m * c
Pęd w zależności od fali
M * v = E/c
stąd E/c = m* c
czyli E = m*c²
Co było do wyprowadzenia.

